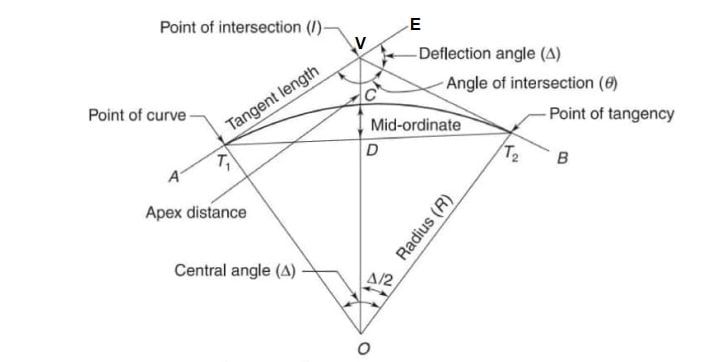
Back Tangent: The tangent line (AT1) before the beginning of the curve is called the Back tangent or the rear tangent.
Froward Tangent: The tangent line (T2B) after the end of the curve is called the Forward tangent. The distinction of the back tangent from the forward tangent depends on the direction of the route surveying.
Point of Intersection (P.I.): The point at which the extension of the back tangent and the forward tangent meet is known as the Vertex (V) or point of intersection (P.I.).
Point of Curvature (P.C.): The point on the back tangent where the curve begins is known as the Point of Curvature (P.C.). At this point, the alignment of the route changes from a straight line to a curve. This is represented by T1
Point of tangency (P.T.): The point on the forward tangent where the curve ends is known as the Point of tangency (P.T.). At this point, the alignment of the route changes from a curve to a straight line.
Intersection angle: The exterior angle at the vertex or point of intersection is known as the Intersection angle ( ). It is also known as the Deflection angle as it represents the deflection angle between the back tangent and the forward tangent. Thus, the angle between the line AV’ produced and the line VB represents the intersection angle or deflection angle.
Deflection angle to any point: The deflection angle to any point on the curve is the angle at P.C between the back tangent and chord from P.C to the point on the curve
Tangent distance (T): The distance between the point of curvature (T1) to the point of intersection (V) along the extension of the back tangent is known as Tangent distance (T). It is also equal to the distance between the points of tangency (T2) to the point of intersection along with the extension of forward tangent.
External distance (E): The distance between the point of intersection (V) and the middle point of the curve is called as External distance (E).
Length of curve (l): The length of the alignment along the curve between the point of curvature (T1) and the point of tangency (T2) is known as the Length of curve (l).
Long chord (L): The longest possible chord of the circular curve is known as Long chord. It is the line joining the point of curvature (T1) and the point of tangency (T2).
Mid ordinate (M): The distance between the middle point of the curve and the middle point of the long chord is Mid-ordinate (M).
Normal Chord (C): A chord between two successive regular stations on a curve. Normally, the length of normal chord is 1 chain.
Sub chord(c): The chord shorter than normal chord is called sub chord. (Fig(1.3.2))
Right hand curve: If the curve deflects to the right of the direction of the progress of survey.
Left hand curve: If the curve deflects to the left of the direction of the progress of survey.
Central angle: The central angle is the angle formed by two radii drawn from the center of the circle (0) the PC and PT. The central angle is equal to the Intersecting angle.
Designation of a Curve:
A curve is designated either in terms of its degree of curvature (D) or by its radius (R).
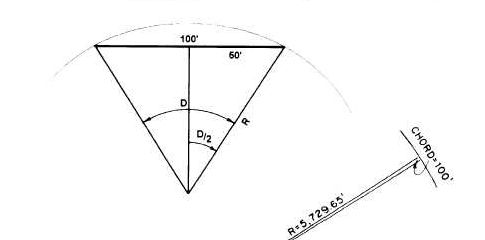
The degree of a curve (D) is defined as the angle subtended at the centre of the curve by a chord or an arc of specified length. The degree of curvature has several slightly different definitions.
Chord Definition:
The degree of a curve is defined as the angle subtended at the centre of the curve by a chord of 100 ft length.
Metric Degree of Curve
In the metric system two degrees of curve are in use:
- Angle at center subtended by an arc of 20m
- Angle at center subtended by an arc of 10m
If the definition is based on 20m
R = 1146/D
If the definition is based on 10m
R = 573/D
Setting out of simple curve:
The various methods used for setting curves may be broadly classified as:
1. Linear methods
In this method, only a chain or tape is used. Linear methods are used when,
- A high degree of accuracy is not required
- The curve is short
The following are some of the linear methods used for setting out simple circular curves:
- Offsets from long chord
- Successive bisection of chord
- Offsets from the tangents–perpendicular or radial
- Offsets from the chords produced.
2. Angular methods
In this method an instrument such as theodolite is used with or without a chain. The following are the angular methods which can be used for setting circular curves:
- Rankine method of tangential (deflection) angles.
- Two-theodolite method
- Tacheometric method
Before setting out of curve it is essential to locate the tangents, point of intersection, point of curvature and point of tangency. Before setting out the curve, the surveyor is always supplied with a working plan upon which the general alignment of tangent is known in relation to the traverse, controlling the survey of the area. Knowing offsets to certain points on both the tangents, the tangents can he staked on the ground the tape measurements. The tangents can be set out by theodolite and the total deflection angle can then be measured by setting theodolite on the P.I. After having located the P.I and measured the tangent length (T) can be calculated from equation
(T) = R tan (D/2)
The point T1 can be located by measuring back a distance VT1 = T on the rear tangent.
Similarly, the point T2, can be located by measuring a distance V T2 = T on the forward tangent.Knowing the chainage of P.I. the chainage of point T1 can be known by subtracting the tangent length from it. The length of the curve is then added to the chainage of T1 to get the chainage of T2.For the ease in calculations and setting out, it is essential that the pegs on the curve are at regular interval from the beginning to the end. Such interval is known as peg interval and the chord joining two such adjacent pegs is known as the full chord or normal chord. The length of the normal chord is generally taken equal to 100 ft in English units or 20 metres in metric units, so that angle subtended by the normal chord at the centre is equal to the degree of the curve. The stations having the chainages in the multiples of chain lengths are known as full stations. The distance between the point T1 and the first peg will be less than the length of the normal chord so that the first chord joining the point of curve T1 to the first peg will be a sub-chord. Similarly, the last chord, joining the last peg on the curve and the tangent point T2 will be a subchord. All other intermediate chords will be normal chords or units chords.
